Differential privacy, an easy case
Explaining the tradeoffs when implementing formal privacy

By law, the Census Bureau is required to keep our responses to its questionnaires confidential. And so, over decades, it has applied several “disclosure avoidance” techniques when it publishes data — these have been meticulously catalogued by Laura McKenna, going back to the 1970 census.
But for 2020, the bureau will instead release its data tables using a “formal privacy” framework known as “differential privacy.”
A unique feature of this new approach is that it explicitly quantifies privacy loss and provides mathematically provable privacy guarantees for those whose data are published as part of the bureau’s tables.
Differential privacy is simply a mathematical definition of privacy. While there are legal and ethical standards for protecting our personal data, differential privacy is specifically designed to address the risks we face in a world of “big data” and “big computation.”
Given its mathematical origins, discussions of differential privacy can become technical very quickly. But a group of scholars from Georgetown, Harvard, MIT, SUNY Buffalo and IBM Research have just published a long article in the Vanderbilt Journal of Entertainment and Technology Law describing differential privacy in more direct language.
They emphasize practical concerns, illustrating how the rigorous nature of differential privacy gives us a framework to think about the potential privacy risks when our data are collected, analyzed and published.
In this note, I will take a similarly direct approach, but instead describe a simple technique for creating differentially private data releases. I hope it will provide a better understanding of the tradeoffs, and offer an easy introduction to other, more complex, processes.
I mean this note as an explainer, offering a sense of what differential privacy is all about. In future posts I will track the debate forming about the impact of the Census Bureau’s choice to adopt differential privacy.
An example
The protection offered by a differentially private system comes from randomness — noise — that is added to data before publishing tables, or the results of other kinds of computations. The more noise, the greater the privacy protection.
Differential privacy introduces an explicit privacy loss parameter that controls how much information is disclosed about us — by choosing its value, we determine the amount of noise we need to add.
Let’s look at an example to make this less abstract. The next table is a small collection of answers from respondents to a “Yes” or “No” question that we would like to keep confidential.

To protect the “Answer” column, we add noise. The randomness will come from a simple game spinner that has dark and light areas — say, the fraction that is dark is 0.45 and the fraction light, 0.55.

We spin once per respondent and if the spinner lands in the dark area we “flip” their answer — a “Yes” becomes a “No,” and a “No” is flipped to a “Yes” — and if it stops in the light area we leave their answer unchanged. In the next table are the respondents’ original answers, the outcomes of each spin, and the flipped or randomized responses.
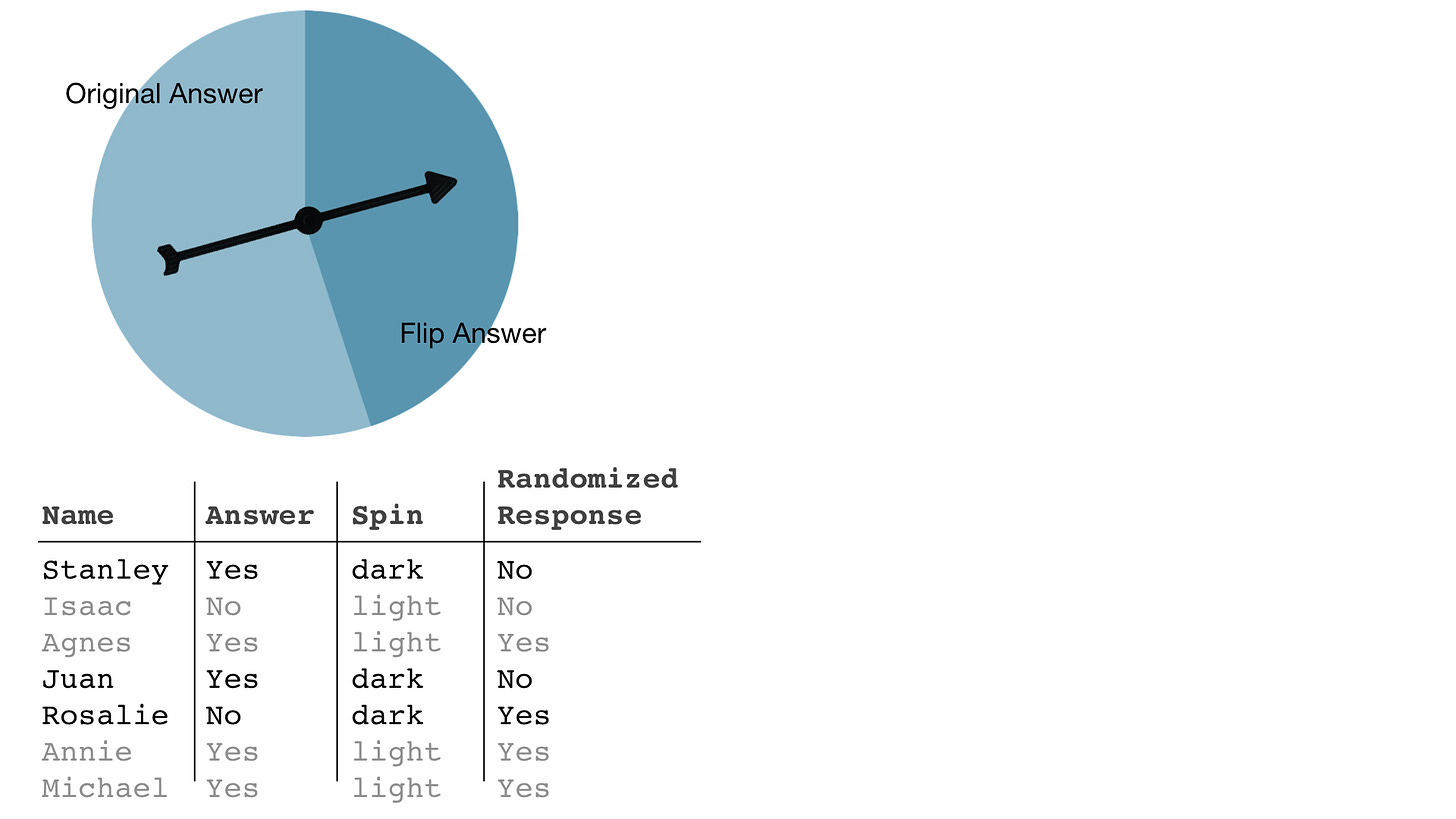
After altering our answers based on the outcome of each spin, the randomized responses are said to be differentially private.
And the privacy comes from uncertainty. A randomized response of “Yes” is essentially as likely to have come from a true answer of “Yes” as it is from a true answer of “No” — providing the spinner is close to 50-50 dark and light. In short, we do not learn very much about an individual respondent’s original answers from their randomized response.
However, as long as we know the precise fraction of the spinner that is light, we can use the randomized responses to estimate something about our group of respondents, like the fraction of people who actually answered “Yes” to the original question.
This is a general feature of differential privacy — each person’s information can be protected, but by knowing the details of how noise was added to the data, we can often perform statistical estimations like counts, averages or even advanced machine learning.
Let’s see how.
Learning from differentially private data
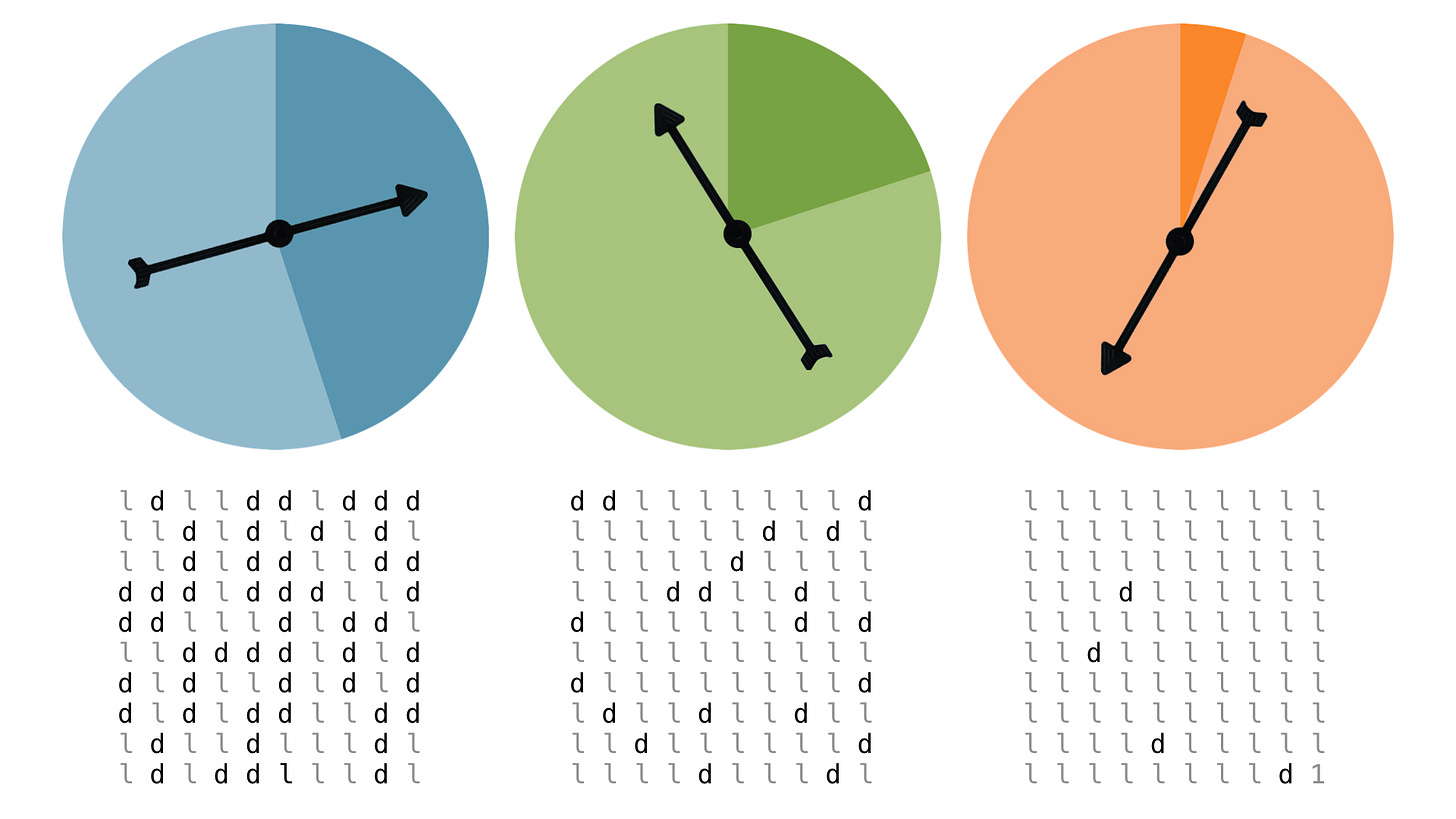
The balance of light and dark is different for each of these spinners. I will use the letter p to refer to the fraction of a spinner that is light, and, in these cases, p = .55, .75 and .95. The blocks of symbols underneath each spinner represent the results of 100 spins where I marked an “l” when the needle fell in the light region and a “d” for the dark.
With p=0.95, just four of the spins landed in the dark area, flipping only four respondents’ answers. Unlike the blue spinner, we are now much more certain about how respondents answered the original question — very little flipping has occurred, and the randomized responses are likely just their true answers. The orange spinner offers little in the way of privacy protection.
Now, for each spinner, because we know the amount of randomness we’ve added, we can use the randomized responses to estimate the fraction of respondents who answered “Yes” in the original data.
Here’s a simple example. Let’s say we have 100 people and 35 of them answer “Yes” to a question. We then use the blue 45-55 spinner to randomize each response — in the block of 100 spins, 49 land in the dark region and we flip the corresponding responses.
To see this in action, in the chart below, pick a position in the first block of “true answers” on the left, find the corresponding spin in the middle block and check the randomized response on the right.

After flipping, 48 of the randomized responses are “Yes.”
The 45-55 spinner offers our respondents a great deal of privacy — there is considerable uncertainty about each person’s original answer. So much so that it would seem this data set is now too noisy to be useful.
But, with a little math, we can combine the fraction of the spinner that is light, p = 0.55, together with the 48 randomized “Yes”s to eke out a little information about the fraction of our respondents who originally answered “Yes.”
Here’s a formula.
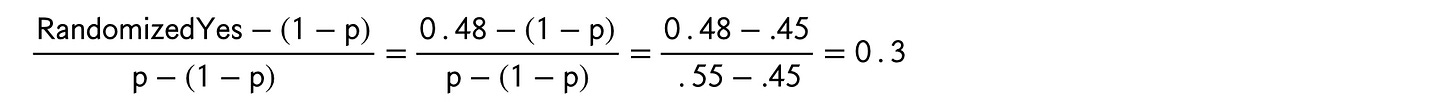
“RandomizedYes” in the equation refers to the the fraction of “Yes”s we see among the randomized responses — in this case we have 48 out of 100, or 0.48. And then p=0.55 for the blue 45-55 spinner.
Let’s try this out for the other spinners to make the calculation clear. In the experiment with the the green 25-75 spinner, we came up with 30 spins landing in the dark region, flipping the corresponding respondents’ answers. This led to 42 randomized “Yes” responses.
And in the experiment using the 5-95 orange spinner, we flipped only 4 answers. And we came up with 36 randomized “Yes”s.
So, for p=0.55 we had 0.48 as the fraction of randomized responses that are “Yes,” for p=0.75 it’s 0.42, and for p=0.05 it’s 0.36. Applying the formula for each, we get the following estimates…

Remember 35 out of 100 of our respondents answered “Yes” to the question originally, and so these estimates seem reasonable — they are all somewhat close to 0.35. However, while it seems that we have a win in all three cases — getting close to the true fraction of respondents who answered “Yes” — these estimates can be quite noisy.
Let’s start with the 45-55 spinner and repeat the 100 spins, flip the original answers according to these new spins, and come up with another estimate. In fact, let’s do the whole thing 10 more times and see what kinds of numbers we get.

One of these is negative and two are larger than 1 — these estimates don’t make any sense if they are to represent the fraction of true “Yes”s in our data set.
But, four of them are smaller than the actual value of 0.35 and six are larger so, while they are noisy, they are at least distributed around the right place.
In fact, after a little math, for the blue 45-55 spinner and 100 people in our data set, we should expect to get estimates that vary around the true value of 0.35, with about 95% of them falling within +/- 1 of 0.35 — that is, we expect our estimates to mostly fall between -0.65 and 1.35. The range is highlighted with a blue bar in the chart. (And yes, anything less than zero or larger than one does not make sense.)

The point is that for the blue spinner we are introducing a lot of randomness and that makes the individual data points less informative — that’s privacy protection at work.
For the green 25-75 spinner, we are flipping less, introducing less noise, and we can expect estimates to vary mostly within just +/- 0.17 of 0.35 — that is, we expect estimates to range from 0.18 to 0.52. Better, but not great. Here are 10 repetitions, and the range is in green in the chart above.

And for the orange 5-95 spinner, our estimates vary mostly around the true value of 0.35 within +/- 0.05 — that is, we expect estimates to range between 0.30 and 0.40, the orange bar in the figure. Here are 10.
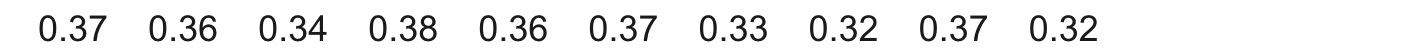
As you can see, there is an explicit price to pay for privacy — accuracy. The blue spinner feels like it offers the greatest uncertainty about whether a particular answer has been flipped or not — the greatest privacy. But with that privacy protection comes a great deal of variation in our estimate. The blue spinner’s low accuracy can even yield nonsensical answers.
That said, differential privacy is designed for large data sets and the accuracy improves as the number of people in the data increases. The chart below makes the progression clear for the blue spinner as we include 1,000 or 10,000 people in our data set instead of just 100.

These are the kinds of tradeoffs we face with differential privacy. The accuracy of estimates depends directly on things like the amount of randomness and the size of the database. Here’s what we’ve learned so far.
It is the introduction of uncertainty that guarantees privacy. The greater the uncertainty, the greater the protection.
The privacy protection is not a property of the final data set we produced, but rather the process we followed to get there.
We can still use a differentially private data set to learn something about the world. Being explicit about the noise mechanism applied, we can form estimates for characteristics of our group of respondents (or a larger population if our respondents are a random sample, as is the case in survey research).
Trading off privacy and accuracy
When I decide to use Google, or to participate in a political survey, or allow my bank to share my data with a third party, I am making a judgement about whether my investment of data is worth the potential loss of my privacy. Outcomes from these data studies are commonly released to the public — they take the form of reports about how many people searched for specific words, or published tabulations from a survey, or even an entire data set that might be posted to GitHub.
How do I assess the privacy risks involved in participating in one of these studies?
Informally, differential privacy provides a guarantee that the conclusions that can be drawn from published outcomes — released tables or other computations — do not change much whether or not I choose to participate in a study. That is, whether or not my data are in the original database. We measure the difference with the greek letter ε.
To make this clear, I have adapted the following figure from the Vanderbilt paper that compares my participating in a study with my choice to “opt-out.”

The difference ε is referred to as the privacy loss parameter. It measures how much extra can be learned if I opt-in, and specifically how much can be learned about me. In turn, it describes how well my data need to be hidden with the addition of noise. The smaller the value of ε I am comfortable with — the lower my acceptable privacy risk — the more noise that has to be introduced for me to participate.
I started this note concerned with the application of differential privacy to situations like the census — we assume people have participated and we would like to protect their answers to our questions. In this case, we can effectively remove a person’s data by replacing their true answer with some default value, say a “Yes” or a “No”. (Technically, a case like the census extends the definition of differential privacy, but the underlying tradeoff between accuracy and privacy remains.)
Again, differential privacy is not a single technique — like our spinners — but a definition that includes a measure for quantifying and managing privacy loss. For a given ε, researchers have developed a number of mechanisms that satisfy this definition — introducing various forms of noise so that an individual’s privacy loss is no more than ε.
This definition and the loss parameter ε allow us to speak meaningfully about privacy and the analysis of data — the parameter ε provides a scale for us to judge privacy loss.
To make this concrete, let’s use our spinner example one last time — here is a chart comparing the light area of our spinner and the privacy loss ε. Notice that for ε of zero, we have a perfect 50-50 light-dark spinner and each data point is essentially noise. There is no privacy loss, but there is also no more information about our questionnaire than there is in a series of fair coin tosses.
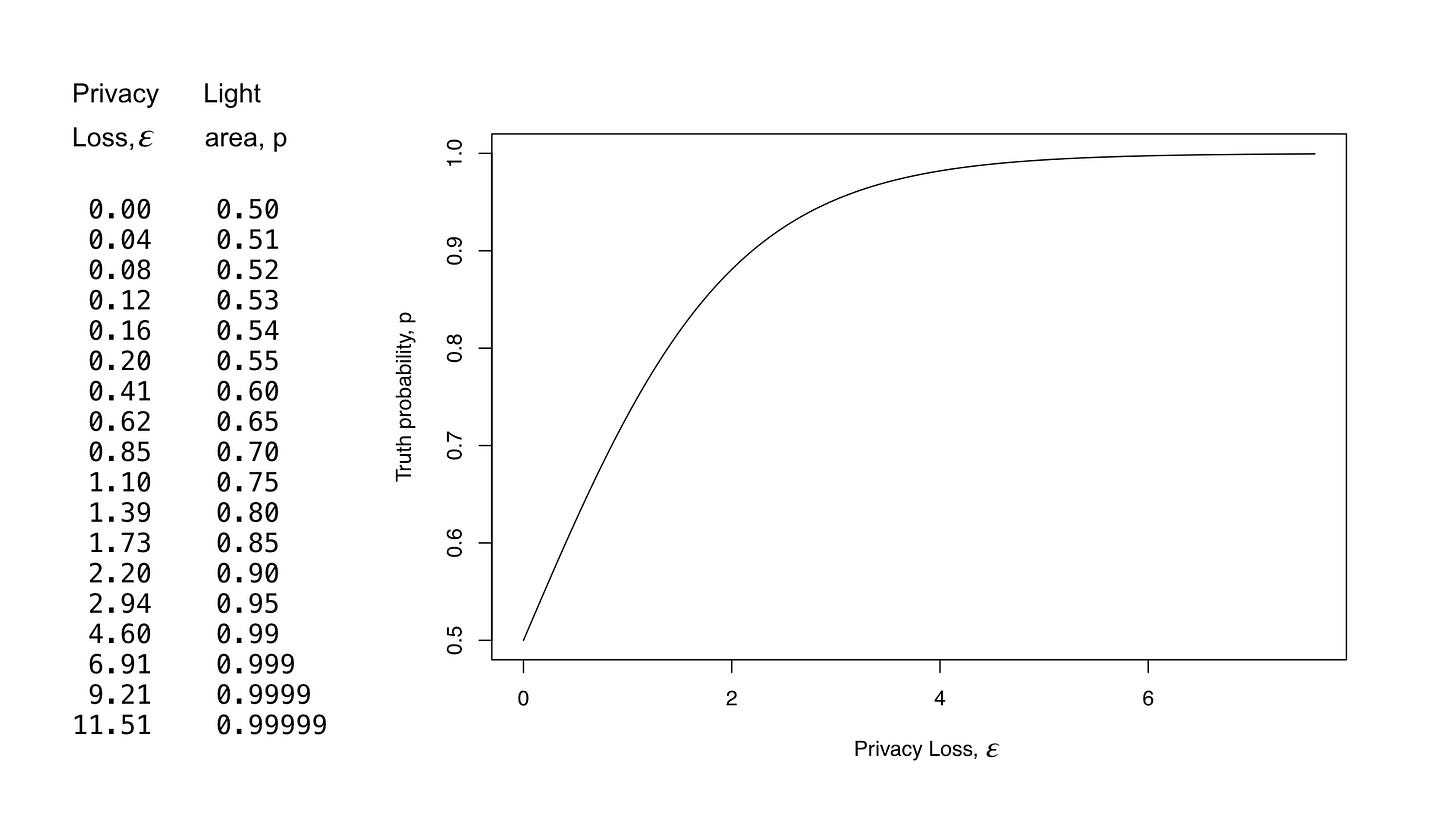
At the other extreme, large values of ε mean spinners that rarely flip respondents’ answers. The accuracy here is high, but the privacy loss is large.
So, when building a data publication system, how would the census or some company choose ε? Cynthia Dwork, one of the inventors of differential privacy, recommends choosing ε small — values like 0.01 and 0.1 — and suggests that you try hard to keep ε less than one.
For its 2018 End-to-End Census Test, for example, the bureau has chosen a value of ε equal to 0.25. That is akin to a 43-57 dark-light spinner. This gives us a sense of the privacy protection. By comparison, one report suggested that Apple’s initial foray into differential privacy for collecting data about usage of its MacOS had an ε of 14.
The process to choose an acceptable loss depends precisely on the tradeoff between accuracy and privacy that we encountered when estimating the true number of “Yes” answers from our randomized data. Legislative district lines, for example, are drawn from census information and can only involve so much noise to be useful. Trading off the amount of noise data-users can tolerate against statutory or other demands to protect the privacy of respondents’ information can be a difficult question.
I have discussed one simple case in which we might release a complete data set, one I describe as “sanitized.” The Vanderbilt paper I alluded to at the beginning of this note also considers situations that are much more interactive, where systems don’t return an entire data set, but instead answer questions about the data. Each subsequent answer can be differentially private and subject to a “privacy loss budget.”
Our spinners can also be applied in a kind of “local” setting, in which data are randomized before sharing with a company or the government — you oversee the privacy step and the organization never sees the original data. This is the approach Apple and Google have taken in their initial applications of differential privacy.
On the other hand, our use case began with the census. This is a different form of data collection, one which involves a “curator” who collects true responses and is trusted to enforce differential privacy safeguards before data are released.
Surveys and sensitive questions
The spinner procedure I described was first proposed by Stanley Warner, a statistician and economist from York University, in 1965. Warner was looking for ways to conduct surveys that included sensitive questions — questions “which demand answers that are too revealing.” Warner wrote
For reasons of modesty, fear of being thought bigoted, or merely a reluctance to confide secrets to strangers, many individuals attempt to evade certain questions put to them by interviewers… Innocuous questions ordinarily receive good response, but questions requiring personal or controversial assertions excite resistance. [There is] a natural reticence of the general individual to confide certain things to anyone — let alone a stranger — and there is also a natural reluctance to have confidential statements on a paper containing his name and address.
Warner originally considered a situation in which a person can either be in a Group A or a Group B — smokers versus non-smokers, frequent versus infrequent gym visitors, excessive use of emoji in email or not. Warner gave each respondent a spinner like the ones I introduced. In his case, the dark area corresponded to group A and the light area group B. After a spin, respondents were then asked to simply report whether the needle was pointing to their group or not.
The result of the spin was known only to the respondent, creating uncertainty about their true answer — Warner referred to this as “plausible-deniability.” The closer to 50-50, dark and light, the more plausible the deniability. Warner hoped this would encourage people to answer difficult questions truthfully. He referred to the technique as randomized response.
The Group A/B framework turns out to be mathematically equivalent to our response flipping — a fact that Warner observed at the end of his paper. He questions which, if either, technique would really encourage respondents to be more truthful in their answers.
Since Warner’s paper, a number of variants of randomized response have been developed, each introducing some uncertainty into whether or not a person’s randomized response represented their true answer. There have also been studies suggesting that this approach, as a survey technique, might not make people feel more comfortable providing personal information, but instead could make them more alert to privacy concerns and prompt them to provide false information.
Note that randomized response is not used in differential privacy to collect data, but instead as part of a processing step before publication. A computer is making the spins and flipping answers, not the respondents. And we don’t have to worry about compliance.
The application of randomized response to differential privacy is outlined in great detail in a paper by Naoise Holohan and Douglas Leith or one by Yue Wang, Xintao Wu and Dongui Hu.
Was this helpful?
I will be writing more frequently on the ways in which the Census Bureau will be using differential privacy in 2020, and the subsequent debates about whether it produces data that are usable by the bureau’s constituents. Future posts will attempt to describe the real-world complications of applying differential privacy on the scale of the census.
More soon!
